1) metapopulation


集合种群
1.
Dynamical analysis of niche construction in n-population metapopulation;


基于生态位构建的n-种群集合种群动态分析
2.
Origin and essence of island biogeography and metapopulation theory;


岛屿生物地理学与集合种群理论的本质与渊源
3.
The symmetric competitive dynamics of metapopulations subject to an Allee-like effect;


集合种群水平上的抽彩式竞争
2) two-metaspecies


2-物种集合种群
1.
Competitive dynamics of two-metaspecies subject to the Allee-like effect;


似Allee效应对2-物种集合种群竞争动态的影响
3) metapopulation dynamics


集合种群动态
1.
Effect of niche construction on metapopulation dynamics by modifying destroyed habitat;


生态位构建通过修复破坏生境对集合种群动态的影响(英文)
2.
Response of metapopulation dynamics to the temporal-spatial heterogeneity of habitat destruction;
集合种群动态对栖息地毁坏时空异质性的响应
4) metapopulation theory


集合种群理论
1.
The origin of metapopulation theory was discussed in this paper,and the latest advance and applied scope were summarized as well.
本文探讨了集合种群理论的形成与成因 ,概述了该理论发展的最新成果及应用前景。
5) metapopulation persistence


集合种群持续
补充资料:集合
| 集合 set 现代数学的一个基本概念。一个集合是指一些事物的全体。简称集。例如,某教室里的全体学生是一个集合,方程x2-x-6=0的所有实根组成一个集合,即-2和3这两个数全体。集合中的事物称为这个集合的元素。a是集合A的元素,作a∈A,“∈”读作属于,a不是集合A的元素,记作 a  A,“ A,“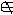 ”读作不属于。由n个事物a1,a2,…,an 组成的集合,常记作a1,a2,…,an。由满足条件P(x)的事物x组成的集合,常表为x|P(x)。如果某种事物不存在 ,就称这种事物的全体是空集。任何空集都是同一个集合,记作 ”读作不属于。由n个事物a1,a2,…,an 组成的集合,常记作a1,a2,…,an。由满足条件P(x)的事物x组成的集合,常表为x|P(x)。如果某种事物不存在 ,就称这种事物的全体是空集。任何空集都是同一个集合,记作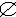 。例如,方程x2+1=0的全体实根组成的集合是空集 。例如,方程x2+1=0的全体实根组成的集合是空集 。组成集合的事物可以是任意指定的。因此,在数学上,一个集合可以是某些数组成的,也可以是某些函数组成的,还可以是平面或空间内某些点组成的,等等。可见集合这个概念是数学的各分支中最基本的概念,研究集合的一般理论对于建立现代数学的基础和推动数学的发展有特殊意义。 。组成集合的事物可以是任意指定的。因此,在数学上,一个集合可以是某些数组成的,也可以是某些函数组成的,还可以是平面或空间内某些点组成的,等等。可见集合这个概念是数学的各分支中最基本的概念,研究集合的一般理论对于建立现代数学的基础和推动数学的发展有特殊意义。给定集合A,如果集合E的元素都是集合A的元素,则称E为A的子集,记作E  A或E A或E A。如果此时E≠A则称E为A的真子集,记作E A。如果此时E≠A则称E为A的真子集,记作E A。A的一切子集构成的集,称为A的幂集,记作P(A)。 A。A的一切子集构成的集,称为A的幂集,记作P(A)。由两个给定集合的全部元素所组成的集合,称为这两个集合的并集。例如集合a,bc,d,e的并集是a,b,c,d,e,集合A和B的并集记做A∪B,读作“A并B”。由两个给定集合的公共元素所组成的集合,称为这两个集合的交集。例如集合a,b,c与集合b,c,d的交集是b,c。集合A和B的交集记作 A∩B 。读作“A交B”。属于集合A而不属于集合B的一切元素组成的集合,称为A与B的差集,记作A/B。例如(x,y)(式中x∈A,y∈B)的一切有序对组成的集合,称为A与B的积集。记作 A×B。例如,欧几里得平面是积集R×R( R是实数集)。这些集合运算渗透到数学的几乎一切领域,成为这些领域内的基本概念。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条