1) diophantine equation


不定方程
1.
About the diophantine equation x~2-3y~4=97;


关于不定方程x~2-3y~4=97
2.
On Diophantine equation x~3+64=21y~2;


关于不定方程x~3+64=21y~2
3.
On the diophantine equation x~2+7=4y~3;


关于不定方程x~2+7=4y~3
2) indeterminate equation


不定方程
1.
Successive solutions to dualistic simple indeterminate equation;


二元一次不定方程的递推解法
2.
An integer solution to one kind to reciprocal indeterminate equation;


一类倒数不定方程的整数解
3.
Fibonacci series and a positive integer solution to an indeterminate equation;


菲波那契数列与一个不定方程的正整数解
3) indefinite equation


不定方程
1.
The Application of Generating Function in Solving Indefinite Equation;


常生成函数在解不定方程中的应用
2.
The positive primitive solution of indefinite equation x~2+my~2=z~2,when m is a square free number;
不定方程x~2+my~2=z~2在m无平方因子时的正本原解
4) integer solution


不定方程
1.
In this paper,the author has proved that the diophantine equation x~3-27=7y~2 has only an integer solution(x,y)=(3,0).
利用递归数列、同余式和平方剩余证明不定方程x~3-27=7y~2仅有整数解(x,y)= (3,0)。
2.
In this paper,the author has proved that the Diophantine equation x~3-1=157y~2has only integer solution(x,y)=(1,0).
用同余法、递归数列证明了不定方程x3-1=157y2仅有整数解(x,y)=(1,0)。
3.
In this paper,the author has proved that the diophantine equationx 2+16 = y 7 has no integer solution.
利用代数数论的方法,证明不定方程x2+16=y7无整数
5) Diophantine equations


不定方程
1.
Then with the help of these results, all solutions of several Diophantine equations in the rings of integers of two quadratic imaginary fields are determined, which implies that the Fermat equation has no non-trivial solutions in these rings.
根据代数数论的理论,将初等数论中的一些结论推广到更大的代数整数环中,应用这些结论确定了几个著名的不定方程在虚二次域的整数环中的解,指出了费尔玛方程在比整数环更大的环中也没有非平凡解。
2.
By using model-theoretic methods,it is verified that one type of the diophantine equations a1xr11+a2xr22+…+anxrnn=bys(a1,a2,…,an,b are integers,r1,r2,…,rn,sare positive integers) have solutions.
用模型论的方法证明了一类不定方程a1xr11+a2xr22+…+anxrnn=bys(其中a1,…,an,b为任意整数,r1,…,rn,s为任意正整数)有解。
3.
All solutions of several important Diophantine equations are determined in a real quadratic field,which implies that the Fermat equation has no non-trivial solutions in this ring when n=4.
确定了几个重要的不定方程在一个实二次域的整数环中的解,指出了费尔玛方程当n等于4时在此环中也没有非平凡解。
6) the system of diophantine equations


不定方程组
1.
On the system of diophantine equations x~2-2y~2=1 and y~2-150z~2=4;


关于不定方程组x~2-2y~2=1,y~2-150z~2=4
2.
On the system of Diophantine equations (m+2)x 2-my 2=2, (4m+4)y 2-(m+2)z 2=3m+2;


关于不定方程组(m+2)x~2-my~2=2,(4m+4)y~2-(m+2)z~2=3m+2
3.
In this paper,it has proved that the system of diophantine equations y~2-10x~2=9 and z~2-17x~2=16 has only integer solution x=0 by using the elementary methods.
文章运用初等证明方法,证明了标题所述的不定方程组只有x=0的整数解。
补充资料:不定方程
| 不定方程 indeterminate equation 未知数个数多于方程个数,且对解有一定限制(比如要求解为正整数等)的方程。数论中最古老的分支之一。古希腊的丢番图早在公元3世纪就开始研究不定方程,因此常称不定方程为丢番图方程。研究不定方程要解决三个问题:①判断何时有解。②有解时决定解的个数。③求出所有的解。中国是研究不定方程最早的国家,公元初的五家共井问题就是一个不定方程组问题,公元5世纪的《 张丘建算经》中的百鸡问题标志中国对不定方程理论有了系统研究。秦九韶的大衍求一术将不定方程与同余理论联系起来。百鸡问题说:“鸡翁一,直钱五,鸡母一,直钱三,鸡雏三,直钱一。百钱买百鸡,问鸡翁、母、雏各几何?”。设x,y,z分别表鸡翁、母、雏的个数,则此问题即为不定方程组 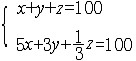
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |