1) periodic parabolic system


周期抛物系统
2) Periodic parabolic systems with delay


含时滞的周期抛物系统
1.
EXISTENCE OF PERIODIC SOLUTIONS AND ASYMPTOTIC BEHAVIOR OF SOLUTIONS ——Periodic parabolic systems with delays;
周期解的存在性和解的渐近性——含时滞的周期抛物系统
3) parabolic system


抛物系统
1.
The stability of a delayed stage-structured parabolic system with feedback controls;


一类具反馈控制和时滞阶段结构抛物系统的稳定性
2.
Behaviors of solutions to a parabolic system describing a cooperating model with nonlocal sources;
具有非局部源的互惠模型抛物系统解的性质
3.
Blowing up of nonnegative classical solution to a parabolic system;


一个抛物系统非负古典解的爆破
4) parabolic systems


抛物系统
1.
Identifications of parameters in parabolic systems;


抛物系统的参数识别问题(英文)
5) Periodic parabolic operators


周期抛物型算子
6) periodic system


周期系统
1.
Satisfactory estimation of linear discrete periodic systems;


线性离散周期系统满意估计
2.
Energy Storage And Power Flow In Periodic System;


周期系统的电磁储能与功率
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程  (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式  热传导方程初值问题的解可用基本解叠加而成,即  的解为 的解为  极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 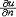 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条