1) first-order predicate expression


一阶谓词公式
1.
This paper studies the modeling of first-order predicate expression by using predicate/transion system.
研究了利用谓词/变迁系统对一阶谓词公式建模的方法。
3) first-order predicate logic


一阶谓词逻辑
1.
Logical reasoning is the basis of artificial intelligence, the first-order predicate logic belonging to logic is a knowledge representation widely used, therefore,it is a meaningful task to study the reasoning problem of first-order predicate logic.
逻辑推理是人工智能的基础,而逻辑中的一阶谓词逻辑是使用较为广泛的知识表示方法,因此研究一阶谓词逻辑的推理问题是一项很有意义的工作。
4) First order predicate logic


一阶谓词逻辑
1.
With the tool of first order predicate logic, this paper demonstrates that there theoretically exists a winning strategy for games which have two players and end after a fixed number moves to get one s win and the other s loss.
用一阶谓词逻辑的工具证明,那种有两方参与,根据规则在有限步内能确定胜负的游戏,从理论上说,存在必胜的方法。
6) pure predicate calculus of first order


一阶纯谓词演算
补充资料:一阶公式
| 一阶公式 first order formula 一阶逻辑的合式公式,在形式化的一阶语言中递归地定义的公式。设 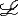 是一阶逻辑的一个形式语言, 是一阶逻辑的一个形式语言,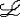 含逻辑符号和非逻辑符号。 含逻辑符号和非逻辑符号。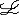 中的非逻辑符号有:关系符号P,Q,R等;函数符号F,G等;常量符号c,d,e等。每个关系符号,函数符号都指定是n元关系或n元函数。 中的非逻辑符号有:关系符号P,Q,R等;函数符号F,G等;常量符号c,d,e等。每个关系符号,函数符号都指定是n元关系或n元函数。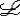 中的逻辑符号有 :个体变元符号 中的逻辑符号有 :个体变元符号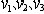 ,…等;逻辑联词 ,…等;逻辑联词 、→等;量词 、→等;量词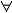 ;等号≡;括号),(。 ;等号≡;括号),(。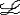 的项t:t可以是单个个体变元,也可以是单个个体常量 :如果t1…tm是项,F是L的m元函数符号,则F(t1…tm)是项。 的项t:t可以是单个个体变元,也可以是单个个体常量 :如果t1…tm是项,F是L的m元函数符号,则F(t1…tm)是项。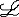 的原子公式:如果t1、t2是 的原子公式:如果t1、t2是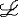 的项,则t1≡t2是 原子公式;如果t1…tn是项,R是L的n元关系符号,则R(t1…tn)是原子公式。 的项,则t1≡t2是 原子公式;如果t1…tn是项,R是L的n元关系符号,则R(t1…tn)是原子公式。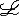 的公式: 的公式: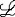 的原子公式是公式;设φ、ψ是L的公式,x是 的原子公式是公式;设φ、ψ是L的公式,x是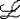 的一个个体变元,则( 的一个个体变元,则( φ),(φ→ψ),( φ),(φ→ψ),(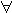 xφ)都是 xφ)都是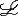 的公式 。这样定义的语言公式乃至公式的集合统称一阶语言 的公式 。这样定义的语言公式乃至公式的集合统称一阶语言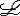 。只要指出 。只要指出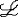 的非逻辑符号,一阶语言 的非逻辑符号,一阶语言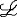 就被确定。 就被确定。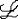 中其他的联结符,量词都不是原始符号,^,ˇ,的定义见命题公式,存在量词定义为xφ 中其他的联结符,量词都不是原始符号,^,ˇ,的定义见命题公式,存在量词定义为xφ  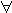 x x φ。一阶公式中的一个个体变元如果出现在量词的辖域中就称为约束变元,不受任何一个量词约束的变元称为自由变元。没有自由变元的公式称为句子。 φ。一阶公式中的一个个体变元如果出现在量词的辖域中就称为约束变元,不受任何一个量词约束的变元称为自由变元。没有自由变元的公式称为句子。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条