1) integral theorem of cauchy


柯锡分定理
2) cauchy integral


柯锡分
3) integral formula of cauchy


柯锡分公式
4) Cauchy integral theorem


柯西积分定理
1.
A class of real integral was solved by using the Cauchy integral theorem.


应用柯西积分定理解决一类实积分的计算问题。
2.
A discussion on some characterized mapping conclusions similar to Cauchy integral theorem.
讨论具有某种特征映射的类似柯西积分定理的结论 。
5) Cauchy theorem


柯西定理
1.
Extension and Application of Cauchy Theorem;


柯西定理的推广及其应用
2.
Cauchy theorem is one important theorem of complex function and there are many reasoning methods demonstrated in the textbook.
柯西定理是复变函数论中的重要定理之一,教材中有多种证法,大多数是在附加导函数连续的条件下给出的,证明不够严密,为此,讨论了一种取消该附加条件后的证法,过程虽复杂,但证明严密、思路清晰。
3.
Based on Cauchy theorem and Rolle theorem, applied structure assist function method has proved the fundamental theorem.
以柯西定理、罗尔定理为基础,应用构造辅助函数法对带有Lagrange余项的泰勒公式进行证明。
6) Koenig theorem


柯尼希定理
1.
Based on the Koenig theorem,the relationship of mechanical energy between pre and post collision has been given.
从柯尼希定理出发,给出了两体碰撞前后的机械能关系,并以两个具体习题为例,说明了利用柯尼希定理求解两体碰撞问题的方法,要比用动量守恒结合能量守恒的方法更为简洁、可行。
2.
The article gives koenig theorem in special relativity on the basis of the centre of momentum define
本文在定义了动心的基础上推导出狭义相对论中的柯尼希定
补充资料:柯西积分定理
| 柯西积分定理 Cauchy's integral theorem 复变函数论的核心定理 。它讨论一个区域D上的复函数在什么条件下在D上积分与路径无关,最简单的柯西积分定理的形式为:当D是单连通区域,而f(z)是D上的解析函数时,以下3个互相等价的结论成立:① f(z) 在D内沿任意可求长曲线积分与路径无关。②f(z)在 D内沿任意可求长闭曲线积分为零。③f(z )在D上有原函数。如果在连续函数类中讨论,则以上定理还是可逆的。柯西定理有以下常用的变化的形式:①D是由几条简单光滑闭曲线围成的有界区域,记L=  D,f(z)在D上解析,在 D,f(z)在D上解析,在 =DUL上连续,则必有 =DUL上连续,则必有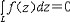 ;②在上述条件下,若L=L0+ ;②在上述条件下,若L=L0+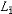 +…+L +…+L 即D由L0, 即D由L0, ,…,L ,…,L 所围成,则 所围成,则 。 。作为柯西积分定理的应用,有同样可作为解析函数充要条件的柯西积分公式:f(z)在  上连续 ,在D内解析的充要条件是 上连续 ,在D内解析的充要条件是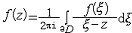 。柯西积分公式是证明一系列解析函数重要性质的工具,首先是证明了圆盘上的解析函数一定可展为幂级数,从而证明了A.-L.柯西与K.魏尔斯特拉斯关于解析函数两个定义的等价性 ,其次证明了解析函数是无限次可微的,从而其实部与虚部也是无限次可微的调和函数。柯西积分定理已推广到沿同伦曲线或沿同调链积分的形式。柯西积分公式在多复变函数中也有许多不同形式的推广。 。柯西积分公式是证明一系列解析函数重要性质的工具,首先是证明了圆盘上的解析函数一定可展为幂级数,从而证明了A.-L.柯西与K.魏尔斯特拉斯关于解析函数两个定义的等价性 ,其次证明了解析函数是无限次可微的,从而其实部与虚部也是无限次可微的调和函数。柯西积分定理已推广到沿同伦曲线或沿同调链积分的形式。柯西积分公式在多复变函数中也有许多不同形式的推广。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条