1) limit information capacity


极限信息容量
2) ultimate information content


极限信息量
1.
The research subject of ultimate information content on a highway guid sign is a important subject for ensure the safety.
公路指路标志信息需求的增加容易导致驾驶员识别信息量过载与标志版面大型化,使驾驶员无法在安全时间内阅读完标志上的信息,因此,公路指路标志极限信息量研究是确保驾驶安全的重要课题。
3) limit capacity


极限容量
1.
Particularly, link budget, propagation model, capacity estimate and the limit capacity and so on are described.
特别对链路预算、传播模型、容量估算和极限容量等进行了阐述,给出了上行极限容量分析及上行链路容量规划的举例。
4) information content


信息容量
1.
The effect of printing stock on the printing quality is analyzed by the study of the maximum information content and the signal to noise of the printing stock.
通过研究纸张的最大信息容量以及与其相关的信噪比,分析了作为承印材料的纸张对印刷品质量的影响。
2.
Being a sub-research project of national nature science fund project "The Uncertainty of DEMs and Their Influence to Applications", this research focus mainly on the concept, theory and methodology of DEM spatial information content.
本研究为国家自然科学基金项目“数字高程模型不确定性及其对应用影响研究”的分支课题,主要探讨DEM空间信息容量研究的基本概念、理论依据与分析方法。
5) Information capacity


信息容量
1.
Constraint relation of the information capacity and the bit error ratio of the binary memoryless digital channel;
二进制无记忆数字信道信息容量与误码率制约关系
2.
The different assessment methods for the gray-scale images resulting from nearinfrared imagery and their different applications were discussed,based on the information capacity,energy spectrum-entropy and false signal-to-noise ratio.
研究了近红外成像所生成的灰度图像的评价方法,分析了基于信息容量、能量谱-熵、伪信噪比的评价方法,以及每种方法所适用的场合,建立了基于静脉图像质量的评价方法。
6) information content


信息内容;信息量
补充资料:极限
| 极限 limit 微积分学乃至分析数学的基本概念之一,用于描述变量在某一变化过程中的变化趋势。极限的朴素思想和应用可追溯到古代,中国早在2000年前就已能算出方形、圆形、圆柱等几何图形的面积和体积,3 世纪刘徽创立的割圆术,就是用圆内接正多边形面积的极限是圆面积这一思想来近似计算圆周率π的。并指出“割之弥细,所失弥少,割之又割,以至不可割,则与圆合体而无所失矣”。随着微积分学的产生,极限概念被明确提出,但含糊不清,直至19世纪,由A.-L.柯西、K.魏尔斯特拉斯等人的工作 ,以及实数理论的建立,才使极限理论建立在严密的理论基础之上。 对于给定的数列 an,如果当n无限增大时,an 有确定的变化趋势棗与某一实数a无限接近,则说数列 an以a为极限,记作 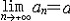 。例如,数列 。例如,数列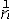 以0为极限,即 以0为极限,即 ,又如 ,又如 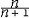 的极限为1,即 的极限为1,即 。数列极限有以下四则运算法则:设 。数列极限有以下四则运算法则:设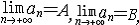 则有 则有 , ,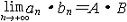 , , 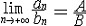 (B≠0)。任给一个数列 an,不一定有极限,例如,1,-1,1,-1,…和2,4,6,…,2n,…,但后一个数列当n无限增大时,an=2n也无限增大,此时也说an趋于正无穷大,记作 (B≠0)。任给一个数列 an,不一定有极限,例如,1,-1,1,-1,…和2,4,6,…,2n,…,但后一个数列当n无限增大时,an=2n也无限增大,此时也说an趋于正无穷大,记作 。 。对于给定的函数y=f(x),如果在x=x0点附近有定义(在x0点可以没有定义),并且当x无限接近x时,f(x)与某一实数A无限接近,则称A为f(x)当x趋向于x0时的极限,记作 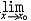 f(x)=A。例如f(x)=x2当x→ f(x)=A。例如f(x)=x2当x→ 的极限为 的极限为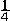 ,又如 ,又如 。函数极限也有以下四则运算法则:设 。函数极限也有以下四则运算法则:设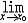 f(x)=A, f(x)=A,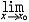 g(x)=B,则有[f(x)±g()]=A±B,f(x)·g(x)=A·B, g(x)=B,则有[f(x)±g()]=A±B,f(x)·g(x)=A·B, (B≠0)。 (B≠0)。 f(x)=A表示当 x无限增大时,f(x)与实数A无限接近,即f(x)以A为极限。 f(x)=A表示当 x无限增大时,f(x)与实数A无限接近,即f(x)以A为极限。函数极限与数列极限有以下关系: 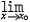 f(x)=A,当且仅当对每一以x0为极限的数列xn,有f(xn)→A(xn≠ x0)。这可以将函数的极限问题转化为数列极限问题来考虑。在某些情况下,是非常有效的。例如,从 f(x)=A,当且仅当对每一以x0为极限的数列xn,有f(xn)→A(xn≠ x0)。这可以将函数的极限问题转化为数列极限问题来考虑。在某些情况下,是非常有效的。例如,从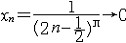 , ,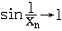 和 和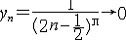 , ,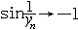 ,可知当 x→0时 , ,可知当 x→0时 ,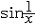 没有极限。 没有极限。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条