1) vibrational natural frequency


振动固有频率
1.
The fluid-solid coupling vibration differential equation of piping system was obtained according to the Hamilton principle,and the approximate analytic formulations of vibrational natural frequency was obtained by using the Galerkin method.
根据Hamilton原理,推导了管路固液耦合振动微分方程,通过Galerkin法,计算出了管路系统振动固有频率的近似解析式。
2) natural vibration frequency


固有振动频率,自振频率
3) free vibration natural frequency


自由振动固有频率
4) Torsional vibration/Natural frequency


扭转振动/固有频率
6) eigentone


本征音;固有振动频率
补充资料:自由振动
| 自由振动 free vibration 系统受初扰动后不再受外界激励时所作的振动。例如单自由度的弹簧振子,其振子质量为m,弹簧的刚度为k,且阻尼可以忽略,则其振动微分方程为mx+kx=0。其解为x=Asin(ωnt+j),式中x为位移;t为时间; 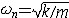 为角频率,它与初始条件无关而取决于系统的参数,也称固有频率 ;A、j分别为振幅和初相位,由振子的初位移x0和初速度 为角频率,它与初始条件无关而取决于系统的参数,也称固有频率 ;A、j分别为振幅和初相位,由振子的初位移x0和初速度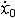 确定: 确定: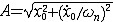 ;j=arctg(ωnx0/ ;j=arctg(ωnx0/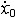 )( )(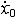 ≥0),j=π+arctg(ωnx0/ ≥0),j=π+arctg(ωnx0/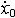 )( )(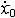 <0)。单自由度系统的无阻尼自由振动是简谐运动,其周期T 和频率f为:T=1/ f=2π <0)。单自由度系统的无阻尼自由振动是简谐运动,其周期T 和频率f为:T=1/ f=2π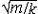 。在无阻尼自由振动的过程中,系统的动能和势能不断地相互转换,且机械能守恒;其振幅决定于系统在起振的时候所具有的能量,且大小保持不变。有阻尼的自由振动参见衰减振动。 。在无阻尼自由振动的过程中,系统的动能和势能不断地相互转换,且机械能守恒;其振幅决定于系统在起振的时候所具有的能量,且大小保持不变。有阻尼的自由振动参见衰减振动。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条